Partha Goswami ^1*

1 University of Delhi, Kalkaji, New Delhi-110019, India.

*Corresponding Author:Partha Goswami, University of Delhi, Kalkaji, New Delhi-110019, India, Tel: +91 22 2576 7230; Fax: +91 (22) 2572 6895; E-mail: physicsgoswami@gmail.com

Citation: Partha Goswami (2022) Investigation of Surface State of Topological Kondo Insulator with Rashba Impurities. Nano Technol & Nano Sci J 4: 131. 

Received: November 28, 2020; Accepted: December 15, 2022; Published: December 19, 2022. 

Copyright: © 2022 Partha Goswami, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

We study a generic topological Kondo insulator (TKI) system by performing a mean-field theoretic (MFT) calculation within the frame-work of slave-boson protocol. We assume infinite Hubbard-type interaction among the localized electrons. The difference between the bulk metallic and insulating phases of TKI is in the sign of nearest neighbor hopping of localized electrons: the hopping amplitude is positive for the metallic and negative for the insulating phase. The surface metallicity together with bulk insulation, however, requires very strong f-electron localization. Furthermore, we find that the exchange field, arising due to the presence of the magnetic impurities on the surface of the system, opens a gap at the gapless Dirac dispersion of the surface states. For the gapped surface state spectrum, we find the possibility of intra-band as well as inter-band unconventional plasmons. The paramountcy of the bulk metallicity, and, in the presence of the Rashba impurities, the TKI surface comprising of ‘helical liquids’ are the important outcomes of the present communication. The access to the gapless Dirac spectrum leads to spin-plasmons with the usual wave vector dependence q1/2. The Rashba coupling does not impair the Kondo screening and does not affect the QCP for the bulk.

The Periodic Anderson model (PAM) [1-6, 25] basically involves highly correlated electrons (localized magnetic  moments) in one of orbital which are screened by weakly correlated electrons in a second d orbital. Although this model has been thoroughly examined for several decades, the model itself and its extensions [5,6] are still relevant for the theoretical condensed-matter physics. A captivating development in recent years is the discovery that Kondo insulators can develop topological order to form a topological Kondo insulator (TKI). The theoretical description of a Kondo insulator [7-10, 16] is usually based on PAM. In this paper we shall focus on a generic topological Kondo insulator with the simplest band structure. Upon including the effect of prototypical Rashba impurities, such as metals or metallic alloys, which bolster the Rashba spin-orbit interaction (RSOI) between f – electrons in the surface state Hamiltonian, we get access to the gapless Dirac spectrum and the spin-plasmons with the usual wave vector dependence q1/2. The Kondo screening in the bulk remains unaffected by RSOI. It may be mentioned that the first example of correlated topological Kondo insulator (TKI) [1,7-10] is SmB6. It has a cubic crystal structure of the cesium-chloride type with a lattice constant of a ≈ 4.13 Å. At high temperature, the material behaves like a metal, but when reducing the temperature below ∼ 50 K, it exhibits insulating behavior [11]. The hybridization gap (?) has been measured at ∼15 meV [11,12]. This constitutes typical behavior for a Kondo insulator. However, SmB6 shows some unusual properties in addition. It has been found [13] that the resistivity of SmB6 increases like an insulator but saturates at temperatures below 5K upon decreasing the temperature. While non-magnetic impurities do not influence the saturation anyway, doping SmB6 with magnetic impurities does [14,15]. The unusual properties of this rare earth hexa-borides are ascribed to the interaction of the 5d and 4f electrons of rare earth element with the 2p conduction electrons of Boron. Unlike the well-known topological insulators, such as Bi2Se3 family of materials, in TKIs the strong correlation effects among the 4f-electrons are very important. It brings about the strong modification of the 4f -band width. It may be mentioned that in the Bi2Se3 family of materials, the band inversion happens between two bands both with the p character and similar band width. The situation in SmB6 is quite different, where the band inversion happens between 5d and 4f bands with the band widths differing by several orders of magnitude, which leads to very unique low energy electronic structure. To investigate the bulk model, the slave boson technique [1,17-20] is usually employed. The slave particle protocol is based on the assumption of spin-charge separation in the strongly correlated electron systems in Mott insulators. The surmise is that electrons can metamorphose into spinons and chargons. But to preserve the fermion statistics of the electrons, the spinon-chargon bound state must be fermionic, so the simplest way is to ascribe the fermion statistics to one of them: if the spinon is fermionic then the chargon should be bosonic (slave-boson), or if the chargon is fermionic then the spinon should be bosonic (slave-fermion). The two approaches are just two low-energy effective theories of the complete-fractionalization theory [21,22]. We use the slave-particle mean-field theory (MFT) [1,12-14] which allows the study of low-energy regime of a Kondo system with a quadratic single-particle Hamiltonian in the limit of the f-electron correlations being larger than all other energy scales in the problem. We obtain the self-consistent equations for MFT parameters minimizing the grand canonical potential of the system with relative to these parameters as in ref. [1]. The parameters enforce constraints on the pseudo-particles due to the infinite Coulomb repulsion and the need of the formation of singlet states between an itinerant electron and a localized fermion at each lattice site in order to have a Kondo insulator. The technique used by us to calculate various thermodynamic averages is the green’s function method as was used by Legner [1]. The theory allows to conveniently circumvent complications associated with formally, infinite repulsion between the f-electrons by “splitting” the physical f-electron into a product of a fermion and a slave boson, supplemented with a constraint to remove the double occupancy. The temperature range that slave-particle mean-field-theory is valid, limited to very low values (T → 0). Furthermore, MFT involves condensing the boson field and neglecting all of its dynamics. This effectively leads to a non-interacting model of an insulator, where the gap is proportional to the condensate and hybridization parameter, and makes it amenable to a topological analysis. Since the electron states being hybridized have the opposite parities, the resulting Kondo insulator is topological and contains its hallmark feature - the metallic surface states. Thus, the mean-field theory is reasonable, and works at the qualitative level. A fundamental quantity describing the magnetic response of the system is the spin susceptibility. The Kondo screening mechanisms are mostly characterized by the same response function. We wish to report the calculation of the bulk spin susceptibility of this system, identified by the dominance of the bulk metallic character, in a sequel to this work. The paper is organized as follows: In section 2, we consider a model for a (topological) Kondo insulator on a simple cubic lattice with one spin-degenerate orbital per lattice site each for d and f electrons with Hubbard type interaction term (U) between the latter. We implement the slave-boson protocol to include the effect of infinite U into consideration at the mean-field theoretic (MFT) level. We obtain the grand canonical potential ? of the system in the slave-boson representation with infinite U. The mean-field parameters, such as slave-boson field, auxiliary chemical potential, and a Lagrange multiplier to enforce the prohibition of double occupancy were obtained by minimizing this grand canonical potential with respect to these parameters. In section 3, we investigate the surface state dispersion followed by the plasmonics of the surface states. Upon including the effect of Rashba impurities on the surface, we get access to the gapless Dirac spectrum and the spin-plasmons. The paper ends with a short discussion and concluding remarks at the end.

The widely accepted model of a topological Kondo insulator (TKI) [7-10, 16] involves, alongside a strong spin-orbit coupling, hybridization between an odd-parity nearly localized band and an even-parity delocalized conduction band. In the case of SmB6 with a cubic crystal structure, these bands correspond to 4f and 5d electrons, respectively. It is then imperative that we start with the periodic Anderson model (PAM) where there are two different species of electrons, namely conduction electrons and localized electrons, often originating from d and f orbitals, respectively. We shall call them the conduction electrons and the valence electrons, respectively. The model [1-6, 8, 25] given below ignores the complicated multiplet structure of the d and f orbitals usually encountered in real TKIs such as SmB6. This has no major implication as most topological properties of cubic Kondo insulators do not depend on the precise form of the hopping and hybridization matrix elements or, on the particular shape of the orbitals.
Model

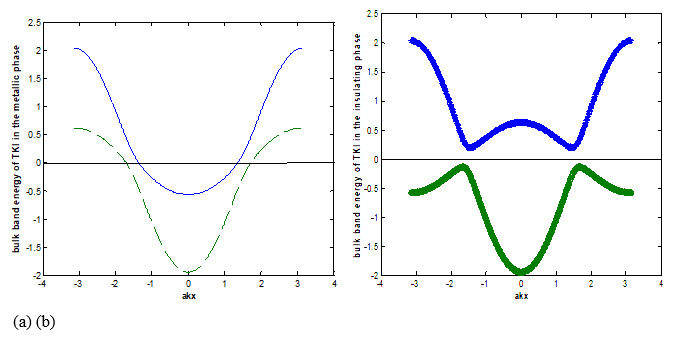
 Figure 1: The two-band energy spectra of a bulk TKI. The parameter values are, ak_y In figure (a), = 0.3. The conduction band is partially empty which implies the bulk metallicity. In figure (b),  In case this case, the Fermi level (Chemical potential represented by solid, horizontal line) is located in the hybridization gap which implies bulk insulation. Our main aim in this paper is to capture physics associated with the inclusion of the Rashba impuritiesin the system, modeled by appropriate surface Hamiltonian derived from the bulk Hamiltonian . The interaction term can be studied non-perturbatively by various methods, including dynamical mean-field theory, Gutzwiller-projected variational wave-functions, or slave-particle representations [1, 29,30]. In what follows we shall use the slave-particle protocol. The f-electron correlations, being larger than all other energy scales in the problem, effectively enforce a no-double-occupancy constraint on each site, and therefore contribute through virtual processes at low temperatures only. The original Hilbert space thus get projected onto a smaller subspace, where the double occupancy is excluded.

One utilizes the well-known slave-boson protocol [1,12-14] to do the projection onto the Hilbert space. In this protocol, the electron operator is expressed in terms of psuedo-fermions and slave-bosons. The operators a^† (heavy slave-boson creation operator) and b^† (light slave-boson creation operator), respectively, creates doubly-occupied and empty bosonic impurity states out of vacuum. The bosons created by b^† are supposed to carry the electron’s charge. The single site fermionic occupation operator is denoted by s^† . This corresponds to a fermionic operator and carry the electron’s spin but no charge. For U→∞ the double occupancy is prohibited, and hence the operators and a will not be under consideration. The connection of the remaining auxiliary operators ( b, s) to the physical f- electron operator is .In the slave-boson mean-field theory of the infinite-U model ( which consists of replacing

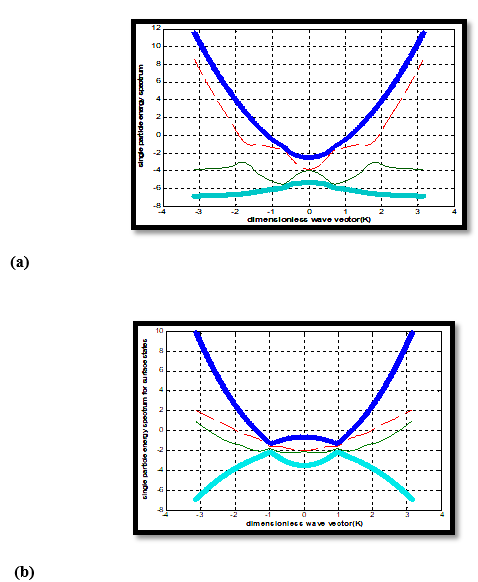
 where  will now be interpreted as the Fermi velocity. It is thus demonstrated that the exchange field can be used to open an additional gap at the surface state dispersion. We now consider the problem of the TKI surface plasmonics. The local variation in charge density in materials gives rise to an electric field. The quanta of in-phase longitudinal density oscillation of charge carriers at the surface of materials driven by this electric field are defined as the surface plasmons (SPs). Inside the bulk, SPs evanesce severely owing to the heavy energy loss. These collective density oscillations can be excited in the conventional metal surfaces. It is clear from the plot of Eq. (25) in Figure 3(b) that the surface could be metallic, even when the bulk is insulating, owing to the conduction bands being partially empty. This is, therefore, an appropriate case to investigate the possibility of the SPs. Equation (27) is expected to yield unconventional q^1/2plasmons [36,37] obtainable under very stringent conditions given by (28). Since the calculation of surface metallicity is in the zero –temperature limit, a prediction of the previous works [7-10] that “when temperature is lowered a Kondo insulator may turn into a topological insulator with a metallic surface state” remains unverified. However, our finding of surface states with gapless Dirac dispersion 

albeit under very stringent conditions corroborates an important experimental finding of Xiang et al.[28]. They have found that, in the case of the prototypical TKI SmB₆, there is a broken rotating symmetry in the amplitude of the main de Haas–van Alphen oscillation branch consistent with Lifshitz-Kosevich theory confirming a 2D nature of the surface electronic state. The finding is similar to quantum oscillation experiments [29,30] for the conventional TIs to probe the surface Dirac fermions. The transport measurements [31] in the past have also demonstrated the insulating bulk and metallic surface separation. For potential applications toward scalable quantum information processing [33] this bulk and surface separation is especially important.

The plasmons are defined as longitudinal in-phase oscillation of all the carriers driven by the self-consistent electric field generated by the local variation in induced charge density? (r,ω). In a linear-response approximation, we have ? (r,ω)=e2∫d^2 r? ?( r,r? ,ω)Φ(r?,ω) where Φ is induced local potential and ? is the fermion response function or the dynamic polarization. This is a quantity of interest for many physical properties, since it determines e.g. the plasmon and phonon spectra. Assuming plasmon oscillation for the 3D system under consideration entirely a surface phenomenon, in the random phase approximation (RPA) [34,35], we write the dynamical polarization function ? (aq,ω) in the momentum space, as

Within the random phase approximation (RPA), the plasmon dispersion is obtained by finding zeros of the dynamical dielectric function, which is expressed in terms of Coulomb’s potential as  where ω’ =ω–¡γ‚γ  is the decay rate of plasmons, the expression ∨(q) is the Fourier transform of the Coulomb potential in two dimensions. For weak damping, the equation Re e (ω’a|q)= 0 yields the plasmon frequency  In the intra-band case, from Eq. (32), in the high frequency imit we obtain

In the present communication we have started with PAM- a model for a generic TKI. The model itself and its extensions are still relevant for the theoretical condensed-matter physics. The examples of extension are those including the on-site interaction between d- and f-electrons and the nearest-neighbour interaction between f-electrons. A stronger version of this on-site interaction is found to destroy the Kondo state and narrow the intermediate valence regime [5], while the latter allows to affect the stability of the magnetic ground state in the Kondo regime [6]. We also have introduced an extension to the model here by way of involving the magnetic exchange interaction. The interaction is introduced in the most direct route using only the spin degrees of freedom. We have demonstrated that the exchange field can be used to open a gap at the surface state dispersion. The field, in fact, is expected to play a bigger role, such as in the efficient tuning of the bulk band gap, the plasmon frequency, and so on. Looking backward, we observe there are many unsettled issues. For example, the problem of hybridization of plasmons with optical surface phonons that is likely to occur when TKI is surrounded by a material other than air has not been addressed. We need to suggest the ways and means to curb such a loss. In conclusion, the inclusion of Rashba impurities in TKI surface gives rise to surface helical states where spin and momentum directions are locked to each other. In the proximity of a superconductor or a magnet, several interesting phenomena, such as the appearance of Majorana anyons, topological Faraday/Kerr effect, fractional charge for the quantum spin Hall effect in 2D, etc. may occur. These offer promising prospects for spintronic applications. Though immense progress has been made in this area over the past decade, never-the-less, we believe that our work may cast new light onto the investigations of how electron correlations and magnetic disorder influence the helical liquid. There are many challenges in the processing of these exotic materials to use the metallic/insulating states in functional devices, and they present great opportunities for the materials science research communities.

Appendix A

The scheme to calculate the averages ?d(k.ζ )^† d_(k,ζ) ?,??bs?_(k.ζ )^† bs_(k,ζ) ?,etc.have been shown in this appendix. For this purpose, we proceed with finite-temperature formalism. Since the Hamiltonian is completely diagonal one can write down easily the equations for the operators {d_(k.ζ )(τ), s_(k,ζ)(τ)},where the time evolution an operator O is given by O(τ)=exp(ℵτ) O exp(−ℵτ ), to ensure that the thermal averages in the equations above are determined in a self-consistent manner. The Green’s functions G_sb (kζ,kζ,τ)= − ??T_τ {d?_(k.ζ ) (τ) ?d^†?_(k,ζ) (0)?, F_sb (kζ, kζ,τ)= − b2??T_τ {s?_(k,ζ) (τ) ?d^†?_(k,ζ) (0)?, etc., where T_τ is the time-ordering operator which arranges other operators from right to left in the ascending order of imaginary time τ, are of primary interest. We find

1. M Legner (2016) Topological Kondo insulators: materials at the interface of topology and strong correlations (Doctoral Thesis), ETH Zurich Research Collection.
2. H Tsunetsugu, M Sigrist, K Ueda (1997) Rev. Mod. Phys 69: 809.
3. P Fazekas (1999) Lecture Notes on Electron Correlation and Magnetism. (World Scientific, Singapore 1999).
4. I Hagymási, K Itai, J Sólyom (2012) Phys. Rev 85: 235116.
5. Y Saiga, T Sugibayashi, D S Hirashima, J Phys (2008) Soc. Japan 77: 114710.
6. S Lamba, R Kishore, S K Joshi (1998) Phys. Rev 57: 5961.
7. M Dzero, Kai Sun, V Galitski, P Colema (2010) Phys. Rev 104: 106408.
8. M Dzero, K Sun, P Coleman, V Galitski ()2012 Phys. Rev 85: 045130.
9. J Werner F, F Assaad (2013) Phys. Rev 88: 035113.
10. J Werner F, F Assaad (2014) Phys. Rev 89: 245119.
11. N Xu, P K Biswas, J H Dil, R S Dhaka, G Landolt et al (2014) Nature Communications, 5: 4566.
12. Weng H, Zhao J, Wang Z, Fang Z, Dai X (2014) et al. Phys. Rev 112: 016403.
13. Deng X, Haule K, Kotliar G (2013) Phys. Rev 111: 176404.
14. Alexandrov V, Dzero M, Coleman P (2013) Phys. Rev 111: 226403.
15. D J Kim, J Xia, Z Fisk (2013) Arxiv 1307.0448
16. D. K. Efimkin and V. Galitski, Phys. Rev. B 90, 081113(R) (2014).
17. A C Hewson (1993) The Kondo Problem to Heavy Fermions. (Cambridge University Press, Cambridge, 1993).
18. P Coleman (1984) Phys. Rev 29: 3035.
19. Partha Goswami, Physica B (2008) Condensed Matter 403: 999-1001.
20. H C Lee, H Yong Choi (2004) Phys. Rev 70: 085114.
21. Kou, Qi,Weng (2005) Phys. Rev 71: 235102.
22. Xu, Sachdev (2010) Phys. Rev 105: 057201.
23. Partha Goswami (1994) Phys. Rev 49: 1600.
24. L P Kadanoff, G Baym (1962) Quantum Statistical Mechanics.
25. M Neupane, N Alidoust, S Y Xu, T Kondo, Y Ishida et al. (2013) Nature Communications.
26. Legner et al. [ M Legner, A Rüegg, M Sigrist (2014) Phys. Rev. 89: 085110 have also derived the surface state dispersion and found that the Fermi velocity for the electrons is vF = 4|V | ( |tf1 td1| (td1 – tf1 )2)1/2 . This result implies that the effective mass of the surface electrons m∗ = pF /vF is quite heavy since the hybridization amplitude is small compared to other relevant energy scale, while the expression under the square root is of the order O (1).
27. Z Zheng, Xu-Bo Zou, G Can Guo (2018) Arxiv: 1802: 09183.
28. Z Xiang, B Lawson, T Asaba, C Tinsman, Lu Chen et al. (2017) 7: 031054.
29. M Z Hasan, C L Kane (2010) Rev. Mod. Phys. 82: 3045
30. X L Qi, S C Zhang (2011) Rev. Mod. Phys. 83, 1057
31. D J Kim, S Thomas, T Grant, J Botimer, Z Fisk et al. (2013) Sci Rep 3: 3150.
32. S Doniach (1968) Adv. In Physics 18: 819.
33. DA Ivanov (2001) Phys. Rev. Lett 86: 268.
34. G Giuliani, G Vignale (2005) Quantum Theory of the Electron Liquid. Liquid (Cambridge University Press, Cambridge, 2005).
35. E H Hwang, S Das Sarma (2007) Phys. Rev 75: 205418.
36. Partha Goswami (2018) International Journal of Modern Physics 13: 1850164.
37. Partha Goswami (2018) “Strong confinement of unconventional plasmons and optical properties of graphene-transition metal dichalcogenide heterostructures”, Journal of Physics Communications 6: 065012.
38. S Raghu, S B Chung, X L Qi, S C Zhang (2010) Phys. Rev 104: 116401.